| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- git
- C# delegate
- gitlab
- 구조체
- c# 윈폼
- 다트 언어
- 유니티
- c# winform
- HTML
- Algorithm
- Unity
- C++
- jupyter lab
- Python
- github
- C언어 포인터
- vim
- Data Structure
- 도커
- jupyter
- 깃
- c#
- 포인터
- Houdini
- Flutter
- docker
- c# 추상 클래스
- 플러터
- c언어
- dart 언어
- Today
- Total
nomad-programmer
[Programming/Algorithm] 기수 정렬(Radix Sort) 본문
기수 정렬은 정렬순서상 앞서고 뒤섬의 판단을 위한 비교연산을 하지 않는다.
비교연산은 정렬 알고리즘의 핵심이라 할 수 있다. 특히 두 데이터 간의 정렬순서상 우선순위를 판단하기 위한 비교연산은 핵심중의 핵심이다. 때문에 모든 정렬 알고리즘들은 이 연산을 포함하고 있다. 뿐만 아니라 알고리즘의 복잡도도 이 연산을 근거로 판단해왔다. 그런데 이런 유형의 비교연산을 하지 않고서도 정렬을 할 수 있는 것이 "기수 정렬"이다.
그리고 정렬 알고리즘의 이론상 성능의 한계는 O(nlog2n)으로 알려져 있는데, 기수 정렬은 이러한 한계를 넘어설 수 있는 유일한 알고리즘이다.
물론 이렇게 좋은 점만 있는 것은 아니다. 다른 알고리즘에는 없는 단점도 있다. 그것은 바로 '적용할 수 있는 범위가 제한적'이라는 것이다. 예를 들어 다음 문장이 말하는 바는 기수 정렬로 해결할 수 있다.
"배열에 저장된 1, 7, 9, 5, 2, 6을 오름차순으로 정렬하라."
반면 다음 문장이 말하는 바는 기수 정렬로 해결할 수 없다.
"배열에 저장된 21, -9, 125, 8, -136, 45를 오름차순으로 정렬하라."
차이가 무엇일까? 다른 예를 살펴보자. 먼저 기수 정렬로 해결할 수 있는 요구사항이다.
"영단어 red, white, black, car, houdini를 사전편찬 순서대로 정렬해라."
반면 다음 문장이 말하는 바는 기수 정렬로 해결할 수 없다.
"영단어 professionalism, polymorphism, far, simple, lhydroxproline을 사전편찬 순서대로 정렬해라."
위의 예를 봤듯이 문제는 '데이터의 길이'이다. 길이가 같은 데이터들을 대상으로는 정렬이 가능하지만, 길이가 같지 않은 데이터들을 대상으로는 정렬이 불가능하다. 물론 정렬의 대상 및 기준에 따라서 특정 알고리즘을 적용하여 길이가 다른 데이터들을 정렬할 수도 있다. 하지만 이 역시 가능한 경우가 매우 제한적이다.
-999 이상 +999 이하의 값들도 기수 정렬의 대상이 될 수 있다. 하지만 이러한 경우 데이터의 가공을 위한 별도의 알고리즘을 고민해야 한다. 뿐만 아니라 별도의 알고리즘 적용으로 인한 효율의 문제도 고민해야 한다.
별도의 알고리즘을 고민하고 효율의 문제를 감수하면서까지 기수 정렬을 사용할 이유가 있을까? 위에서 말했던 '정렬이 불가능하다'는 것이 의미하는 바는 바로 이것이다.
다음의 그림은 한 자리 정수의 정렬과정을 보이고 있다.
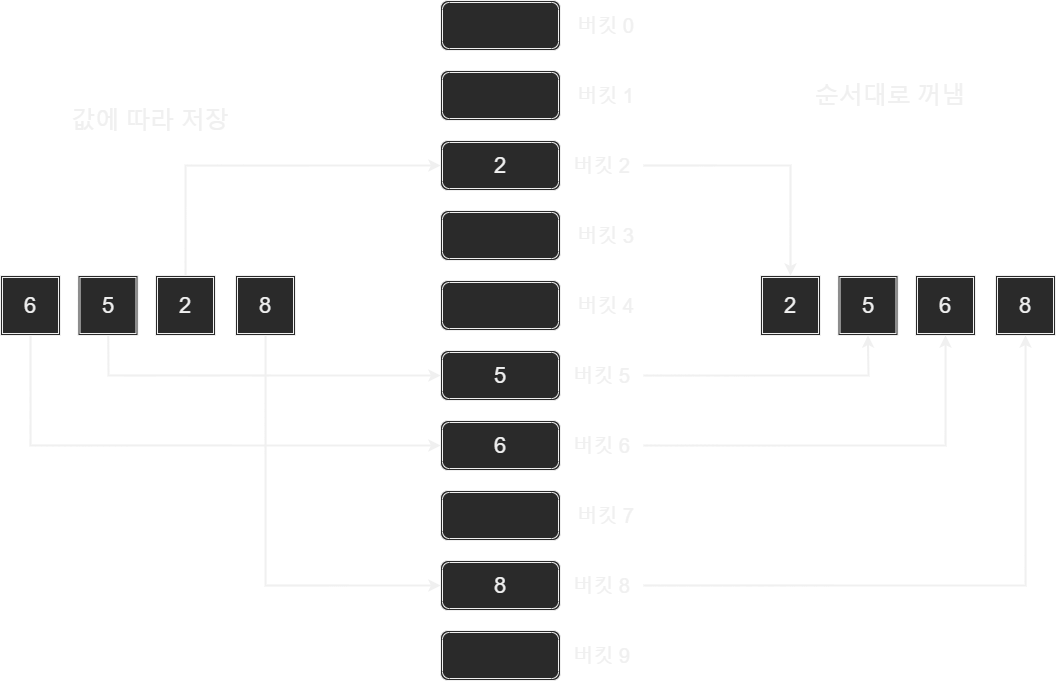
위 그림에서는 10진수 정수의 정렬과정을 보이고 있다. 이렇듯 10진수 정수의 정렬을 위해서는 총 열 개의 '버킷(양동이)'가 필요하다. 버킷은 0부터 9까지 순서대로 이름이 메겨져 있다. 그리고 정렬대상은 값에 해당하는 버킷으로 이동을 한다.
버킷으로의 이동이 끝났다면, 버킷 0에 저장된 것부터 시작해서 버킷 9에 저장된 것까지 순서대로 꺼내서 차례로 나열한다. 간단하다. 이것이 바로 '기수 정렬의 기본 원리'이다.
'기수(radix)'란 주어진 데이터를 구성하는 기본 요소를 의미한다. 예를 들어 2진수는 0과 1의 조합으로 데이터를 표현하니 2진수의 기수는 0과 1이다. 유사하게 10진수는 0부터 9까지의 숫자 조합으로 데이터를 표현하니 0부터 9까지의 숫자가 10진수의 기수가 된다. 그런데 위 그림에서는 기수의 개수만큼 버킷을 마련해서 정렬을 진행하고 있다. 따라서 기수 정렬은 다음과 같이 정의할 수 있다.
기수 정렬(Radix Sort): 데이터를 구성하는 기본 요소, 즉 기수를 이용해서 정렬을 진행하는 방식.
이렇듯 기수 정렬은 기수를 이용한 정렬방식이기 때문에 세 자릿수 정수들을 정렬할 때에도, 이들이 10진수 정수라면, 버킷은 기수의 개수인 10개가 필요하다. 그리고 이는 다섯 자리 정수들이라 해도 마찬가지이다.
그러면 영단어를 정렬해야 한다면, 그것도 아스키 코드의 특수문자를 포함하는 영단어라면 총 몇 개의 버킷이 필요한가? 이 질문을 통해서 간다하게나마 기수 정렬의 단점을 이해할 수 있을 것이다.
기수 정렬의 구현을 목적으로 다음 세 자릿수 정수들을 대상으로 오름차순 기수 정렬을 진행해 보자. 한가지 주의할 점은 이들이 5진수로 표현되었다는 것이다. 이는 다섯 개의 버킷만을 가지고 기수 정렬의 과정을 보이기 위함이다.
134, 224, 232, 122
지금부터 보이는 방법을 가리켜 'LSD 기수 정렬'이라 한다. LSD는 "Least Significant Digit"의 약자로 '덜 중요한 자릿수'에서부터 정렬을 진행해 나간다는 의미를 담고 있다. 쉽게 말해 첫 번째 자릿수부터 시작해서 정렬을 진행해 나간다는 의미이다. 그럼 LSD 기수 정렬의 첫 번째 과정을 살펴보자.
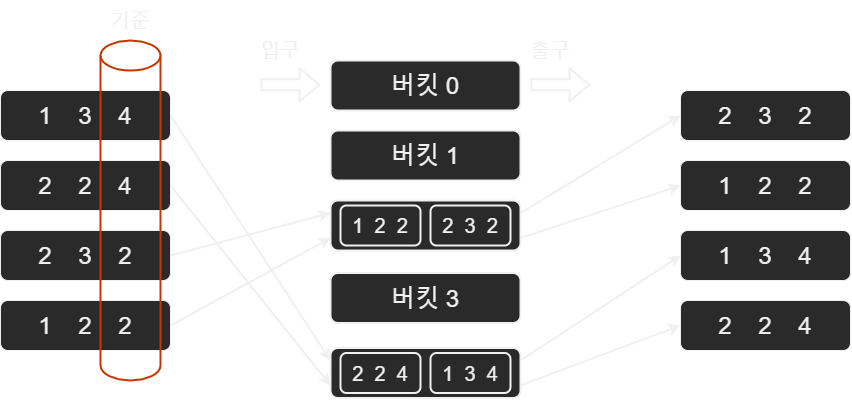
위 그림에서 보이듯이 첫 번째 자릿수를 기준으로 하여 134와 224를 순서대로 버킷 4에 넣고, 이어서 232와 122를 버킷 2에 넣는다. 이제 할 일은 버킷 0에서부터 시작해서 데이터를 꺼내는 것인데, 하나의 버킷에 둘 이상의 데이터가 존재하는 경우 들어간 순서대로 꺼내면 된다. 그리하면 232, 122, 134, 224의 순으로 데이터들은 정렬이 된다.
이제 이들을 대상으로 두 번째 자릿수를 기준으로 정렬을 진행할 차례이다. 그리고 그 과정은 다음과 같다.

위 그림에서 보이듯이 첫 번째 과정과 두 번째 과정의 유일한 차이점은 두 번째 자릿수가 정렬의 기준이라는 점이다. 그러면 이어서 마지막 과정을 살펴보자. 마지막 과정에서는 두 번째 과정의 진행결과를 대상으로 세 번째 자릿수를 기준으로 정렬을 진행한다.
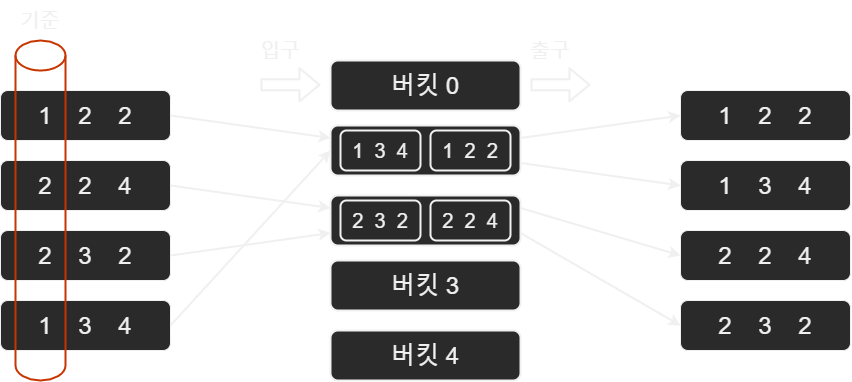
이로써 오름차순으로의 정렬이 완료되었다. 그런데 위의 과정이 간단하긴 하지만 익숙지는 않을 것이다. 왜냐하면 수의 대소를 비교할 때 큰 자릿수부터 비교하는데 익숙하기 때문이다.
예를 들어 324와 421의 대소를 비교할 때, 가장 큰 자릿수인 3과 4만 보고선 421이 크다고 바로 판단을 해버린다. 그런데 위에서 보인 방법은 작은 자릿수에서부터 대소 비교를 진행한다. 대소 비교에 있어서 가장 영향력이 작은 자릿수부터 비교를 하는 것이다. 때문에 이 방법에는 다음과 같은 단점이 있다.
"작은 자릿수에서 시작해서 가장 큰 자릿수까지 모두 비교를 해야 값의 대소를 판단할 수 있다. 비교 중간에 대소를 판단하는 것은 불가능하다."
가장 영향력이 큰 자릿수를 마지막에 비교하니 마지막까지 결과를 알 수 없는 것이 이 방법의 단점이다. 하지만 이러한 단점이 프로그래밍을 하는데 있어서는 장점이 된다.
기수 정렬(Radix Sort) : LSD vs MSD
LSD와 반대의 방향으로 정렬을 진행하는 MSD 기수 정렬을 살펴보도록 하자. LSD 기수 정렬의 결과를 정리하면 다음과 같다.
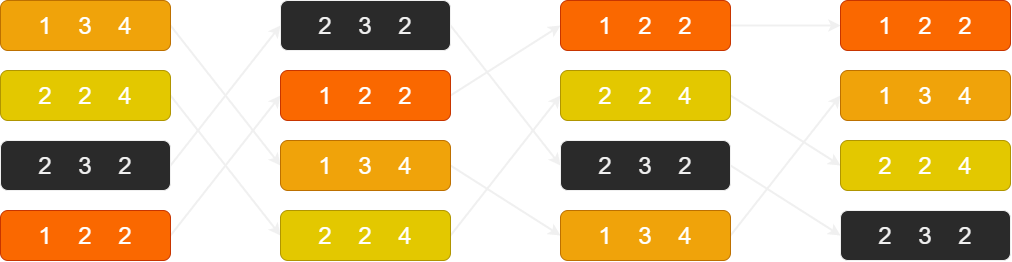
이어서 소개할 'MSD 기수 정렬'의 MSD는 "Most Significant Digit"의 약자로써 가장 중요한 자릿수, 다시 말해 가장 큰 자릿수에서부터 정렬이 진행된다는 의미를 담고 있다.

위 그림이 보여주는 잘못된 결과를 통해서 MSD 방식을 짐작할 수있다. MSD는 가장 큰 자릿수에서부터 정렬이 시작된다. 따라서 LSD와 달리 첫 번째 과정만 거쳐도 대략적인 정렬의 결과가 눈에 보인다. 그리고 이는 단계를 거듭하면서부터 더 확실해진다.
즉 LSD는 미자막에 가서 정렬순서를 판단하는 방식인 반면, MSD는 점진적으로 정렬을 완성해가는 방식이다. 때문에 MSD 방식의 가장 큰 장점은 다음과 같다.
"반드시 끝까지 가지 않아도 된다. 중간에 정렬이 완료될 수도 있다."
이렇듯 마지막까지 비교를 하지 않아도 되니, 성능적 측면에서 이점을 기대할 수 있다. 하지만 다음과 같은 단점이 존재한다.
"모든 데이터에 일괄적인 과정을 가치게 할 수 없다."
잘못된 결과를 보이는 위의 그림을 보자. 224와 232의 정렬순서는 이미 두 번째 과정에서 판별이 났다. 두 번째 자릿수인 2개 3보다 앞서기 때문이다. 그리고 그 결과는 세 번째 자릿수에 영향을 받지 않는다. 따라서 여기서 멈췄어야 했다. 멈추지 않고 마지막 단계까지 진행을 했기 때문에 잘못된 결과를 초래한 것이다.
이러한 요류를 범하지 않으려면, MSD 방식에서는 중간에 데이터를 점검해야 한다. 정렬대상의 일부는 다음 단계로 넘어가된 일부는 넘어가면 안 되는 상황도 빈번히 등장하기 때문이다. 따라서 구현의 난이도가 LSD에 비해 상대적으로 높다. 게다가 중간에 데이터를 점검해야 하므로 성능의 이점도 반감될 수 있다.
기수 정렬(Radix Sort) : LSD 기준 구현
일반적으로 '가수 정렬'이라 하면 LSD 방식을 기준으로 이야기한다. 이는 위에서 말한 '구현의 편의성'이 가장 큰 이유일 것이다.
LSD와 MSD의 빅-오는 같다. 물론 MSD의 경우 정렬의 과정이 단축될 수 있어서 성능의 향상을 조금이라도 기대할 수 있지만, 모든 데이터에 일괄적인 과정을 거치게 할 수 없기 때문에 추가적인 연산과 별도의 메모리가 요구된다. 따라서 일반적인 상황이라면 굳이 MSD 방식을 고집할 이유가 없다. 따라서 LSD 방식의 기수 정렬을 구현하자.
양의 정수라면 그 길이에 상관없이 정렬의 대상에 포함시킬 수 있는 기수 정렬을 구현하고자 한다. 그런데 이는 어렵지 않다. 예를 들어 다음 두 정수를 정렬한다고 가정해보자.
42, 715
LSD 방식이니 처음에는 2와 5를 가지고, 두 번째에는 4와 1을 가지고 정렬의 과정을 진행해야 한다. 즉 처음에는 2와 5를 추출할 수 있어야 하고, 두 번째에는 4와 1을 추출할 수있어야 한다. 그리고 마지막으로 42로부터 0을 715로부터 7을 추출해서 정렬의 마지막 과정을 진행할 수 있으면 된다. 그럼 첫 번째 자리 숫자부터 세 번째 자리 숫자까지의 추출방법을 알아보자.
- NUM으로부터 첫 번째 자리 숫자 추출 : NUM / 1 % 10
- NUM으로부터 두 번째 자리 숫자 추출 : NUM / 10 % 10
- NUM으로부터 세 번째 자리 숫자 추출 : NUM / 100 % 10
어렵지 않은 수식이다. 그리고 수식간 규칙도 단순하다. 특히 세 번째 자리 숫자의 추출을 위해서 NUM에 42를 넣으면 그 결과로 0이 추출됨에 주목해야 한다. 그럼 이어서 위의 수식을 바탕으로 한 기수 정렬의 예를 보자. 참고로 버킷은 그 구조가 큐에 해당하기 때문에 아래의 구현에서는 '연결 리스트 기반의 큐'를 활용하였다.
연결 리스트 기반의 Queue
ListBaseQueue.h
// ListBaseQueue.h
#ifndef __LIST_BASE_QUEUE_H__
#define __LIST_BASE_QUEUE_H__
typedef int Data;
typedef struct _node {
Data data;
struct _node* next;
} Node;
typedef struct _lQueue {
Node* front;
Node* rear;
} LQueue;
typedef LQueue Queue;
void QueueInit(Queue* pq);
int QIsEmpty(Queue* pq);
void Enqueue(Queue* pq, Data data);
Data Dequeue(Queue* pq);
Data QPeek(Queue* pq);
#endifListBaseQueue.cpp
// ListBaseQueue.cpp
#include <iostream>
#include <cstdlib>
#include "ListBaseQueue.h"
void QueueInit(Queue* pq) {
pq->front = nullptr;
pq->rear = nullptr;
}
int QIsEmpty(Queue* pq) {
if (pq->front == nullptr) {
return true;
}
return false;
}
void Enqueue(Queue* pq, Data data) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->next = nullptr;
newNode->data = data;
if (QIsEmpty(pq)) {
pq->front = newNode;
pq->rear = newNode;
}
else {
pq->rear->next = newNode;
pq->rear = newNode;
}
}
Data Dequeue(Queue* pq) {
Node* delNode;
Data retData;
if (QIsEmpty(pq)) {
std::fputs("Queue Memory Error!", stderr);
exit(-1);
}
delNode = pq->front;
retData = delNode->data;
pq->front = pq->front->next;
free(delNode);
return retData;
}
Data QPeek(Queue* pq) {
if (QIsEmpty(pq)) {
std::fputs("Queue Memory Error!", stderr);
exit(-1);
}
return pq->front->data;
}기수 정렬 코드
#include <iostream>
#include <cstdlib>
#include "ListBaseQueue.h"
using std::cout;
using std::cin;
using std::endl;
// 10진수
#define BUCKET_NUM 10
// 매개변수 maxLen에는 정렬대상 중 가장 긴 데이터의 길이 정보 전달
void RadixSort(int arr[], const int num, const int maxLen) {
Queue buckets[BUCKET_NUM];
int divfac = 1;
int radix;
// 총 10개의 버킷 초기화
for (int bi = 0; bi < BUCKET_NUM; bi++) {
QueueInit(&buckets[bi]);
}
// 가장 긴 데이터의 길이만큼 반복
for (int pos = 0; pos < maxLen; pos++) {
// 정렬대상의 수만큼 반복
for (int di = 0; di < num; di++) {
// N번째 자리의 숫자 추출
radix = (arr[di] / divfac) % 10;
// 추출한 숫자를 근거로 버킷에 데이터 저장
Enqueue(&buckets[radix], arr[di]);
}
// 버킷 수만큼 반복
for (int bi = 0, di = 0; bi < BUCKET_NUM; bi++) {
// 버킷에 저장된 것 순서대로 다 꺼내서 다시 arr에 저장
while (!QIsEmpty(&buckets[bi])) {
arr[di++] = Dequeue(&buckets[bi]);
}
}
// N번째 자리의 숫자 추출을 위한 피제수의 증가
divfac *= 10;
}
}
int main() {
int arr[] = { 18, 272, 14, 7141, 5, 15 };
int len = sizeof(arr) / sizeof(int);
for (int i = 0; i < len; i++) {
cout << arr[i] << ' ';
}
cout << endl;
RadixSort(arr, len, 5);
for (int i = 0; i < len; i++) {
cout << arr[i] << ' ';
}
cout << endl;
return 0;
}
/* 결과
18 272 14 7141 5 15
5 14 15 18 272 7141
*/위의 함수 RadixSort는 길이가 가장 긴 데이터의 길이 정보를 전달받도록 정의하였다. 물론 함수 내에서 길이 정보를 직접 계산하도록 구현할 수도 있지만, 그렇게 되면 불필요한 연산을 수반할 수 있어서 위와 같이 정의하였다.
기수 정렬(Radix Sort) : 성능평가
기수 정렬은 비교연산이 핵심이 아니다. 오히려 버킷으로의 데이터 삽입과 추출이 핵심이다. 따라서 이 정렬의 시간 복잡도는 삽입과 추출의 빈도수를 대상으로 결정해야 한다. 이를 위해서 RadixSort 함수를 다음과 같이 정리하였다.
void RadixSort(int arr[], int num, int maxLen) {
...
// 가장 긴 데이터의 길이만큼 반복
for(int pos=0; pos<maxLen; pos++) {
// 정렬대상의 수만큼 버킷에 데이터 삽입
for(int di=0; di<num; di++) {
// 버킷으로의 데이터 삽입 진행
}
// 정렬대상의 수만큼 버킷으로부터 데이터 추출
for(int bi=0, di=0; bi<BUCKET_NUM; bi++) {
// 버킷으로부터의 데이터 추출 진행
}
...
}
}위에서 버킷을 대상으로 하는 데이터의 삽입과 추출을 한 쌍의 연산으로 묶으면, 이 한 쌍의 연산이 수행되는 횟수는 다음과 같다.
maxLen * num
따라서 정렬대상의 수가 n이고, 모든 정렬대상의 길이가 l이라 할 때, 시간 복잡도에 대한 기수 정렬의 빅-오는 다음과 같다.
O(ln)
물론 이는 O(n)으로 보아도 된다. 그리고 이로써 기수 정렬은 O(nlog2n)인 퀵 정렬보다 뛰어난 O(n)의 성능을 보임을 확인하였다. 물론 적용 가능한 대상이 제한적이라는 단점이 있다.
'Programming > Algorithm' 카테고리의 다른 글
| [Programming/Algorithm] 이진 탐색 트리 (Binary Search Tree) (0) | 2021.03.21 |
|---|---|
| [Programming/Algorithm] 탐색의 이해와 보간 탐색 (0) | 2021.03.15 |
| [Programming/Algorithm] 퀵 정렬(Quick Sort) (2) | 2021.03.11 |
| [Programming/Algorithm] 병합 정렬(Merge Sort) (0) | 2021.03.09 |
| [Programming/Algorithm] 힙 정렬(Heap Sort) (0) | 2021.03.09 |




