| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- vim
- Flutter
- 구조체
- C# delegate
- dart 언어
- C++
- github
- 도커
- c언어
- Algorithm
- c# 윈폼
- 포인터
- 유니티
- git
- 플러터
- c#
- Python
- Data Structure
- c# winform
- Houdini
- jupyter
- jupyter lab
- gitlab
- C언어 포인터
- Unity
- 깃
- c# 추상 클래스
- HTML
- 다트 언어
- docker
- Today
- Total
nomad-programmer
[Programming/Algorithm] 우선순위 큐와 Heap 자료구조 본문
Queue의 핵심 연산 두 가지는 다음과 같다.
- enqueue : 큐에 데이터를 삽입하는 행위
- dequeue : 큐에서 데이터를 꺼내는 행위
이와 마찬가지로 '우선순위 큐'의 핵심 연산 두가지도 다음과 같다.
- enqueue : 우선순위 큐에 데이터를 삽입하는 행위
- dequeue : 우선순위 큐에서 데이터를 꺼내는 행위
반면 연산의 결과에는 차이가 있다. 큐는 연산의 결과로 먼저 들어간 데이터가 먼저 나오지만, 우선순위 큐의 연산결과는 다음과 같다.
들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나온다.
우선순위 큐를 구현하는 방법은 다음과 같이 세 가지로 구분할 수 있다.
- 배열을 기반으로 구현하는 방법
- 연결 리스트를 기반으로 구현하는 방법
- 힙(heap)을 이용하는 방법
힙(Heap)이란?
힙은 '이진 트리'이되 '완전 트리'이다. 그리고 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나 같아야 한다. 즉 root 노드에 저장된 값이 가장 커야 한다.
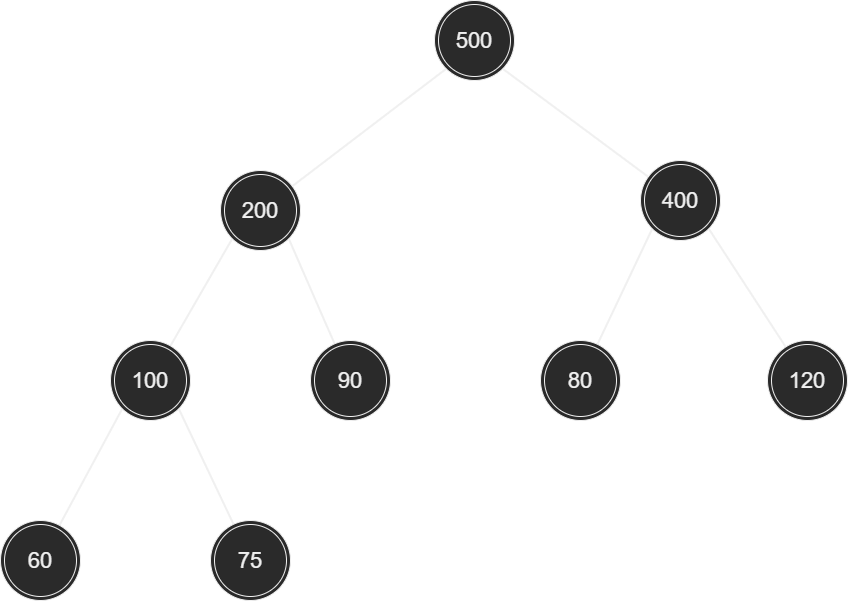
위와 같이 root 노드로 올라갈수록 저장된 값이 커지는 완전 이진 트리를 가리켜 '최대 힙(max heap)'이라 한다. 반면 다음 그림과 같이 root 노드로 올라갈수록 저장된 값이 작아지는 완전 이진 트리를 가리켜 '최소 힙(min heap)'이라 한다.

이렇듯 힙은 root 노드에 우선순위가 가장 높은 데이터를 위치시킬 수 있는 자료구조이니, 이를 기반으로 하면 우선순위 큐를 간단히 구현할 수 있다.
힙(heap)은 무엇인가를 쌓아 놓은 더미와 흡사하다 하여 지어진 이름이다. 영단어 heap은 '무엇인가를 차곡차곡 쌓아 올린 더미' 라는 뜻이다.
힙은 구현은 곧 우선순위 큐의 완성으로 이어진다. 따라서 힙과 우선순위 큐를 동일하게 인식하는 경향이 매우 강하다. 하지만 이는 정확하지 않은 것이다.
힙은 우선순위 큐의 구현에 딱 어울리는, 완전 이진 트리의 일종이라는 사실을 기억하도록 하자.
성능 평가
우선순위 큐의 구현에 있어서 단순 배열이나 연결 리스트보다 힙이 더 적합한 이유는 성능에 있다.
- 배열 기반 데이터 저장의 시간 복잡도 : O(n)
- 배열 기반 데이터 삭제의 시간 복잡도 : O(1)
우선순위가 낮은 데이터를 배열에 저장하는 경우, 배열에 저장된 모든 데이터의 우선순위 비교과정을 거쳐야 하므로 데이터 저장의 시간 복잡도는 O(n)이 되고, 삭제의 과정에서는 맨 앞의 저장된 데이터를 삭제하면 되기 때문에, 이 경우의 시간 복잡도는 O(1)이 된다. 이와 유사하게, 연결 리스트 기반의 우선순위 큐의 성능도 다음과 같이 정리할 수 있다.
- 연결 리스트 기반 데이터 저장의 시간 복잡도 : O(n)
- 연결 리스트 기반 데이터 삭제의 시간 복잡도 : O(1)
우선순위가 높을 수록, 데이터를 연결 리스트의 앞 부분에 배치하는 방식이므로 배열의 경우와 다를 바가 없다. 하지만 힙의 경우는 삽입이나 삭제의 경우 동반되는 비교연산은 주로 부모 노드와 자식 노드 사이에서 일어난다. 그리고 이것이 의미하는 바는 다음과 같다.
"힙은 기반으로 하면 트리의 높이에 해당하는 수만큼만 비교연산을 진행하면 된다."
- 힙 기반 데이터 저장의 시간 복잡도 : O(log2n)
- 힙 기반 데이터 삭제의 시간 복잡도 : O(log2n)
힙은 완전 이진 트리이므로, 힙에 저장할 수 있는 데이터의 수는 트리의 높이가 하나 늘 때마다 두 배씩 증가한다. 때문에 데이터의 수가 두 배 늘 때마다, 비교연산의 횟수는 1회 증가한다. 바로 이 사실을 근거로 위의 결론을 내릴 수 있다.
이것으로 우선순위 큐의 구현에 있어서 배열/연결 리스트 보다도 힙(heap)이 어울리는 이유를 객관적으로 알 수 있다. 알고리즘 성능에 있어서 O(n)와 O(log2n)의 차는 엄청난 차이이다.
힙은 트리이다. 트리를 구현하는 방법에는 '배열'을 이용하는 방법과 '연결 리스트'를 이용하는 방법이 있다. 그래서 배열과 연결 리스트 중 하나를 선택해야 한다.
힙의 구현은 배열을 기반으로 구현하는 것이 원칙으로 여겨지고 있다. 그 이유는 다음과 같다.
"연결 리스트를 기반으로 힙(heap)을 구현하면, 새로운 노드를 힙의 '미자막 위치'에 추가하는 것이 쉽지 않다."
사소한 이유 같고, 그래서 연결 리스트를 기반으로도 쉽게 해결 가능한 문제처럼 보이지만, 이는 결코 간단한 무넺가 아니다. 하지만 배열 기반의 힙이라면 이는 매우 간단한 문제가 된다. 그래서 힙과 같이, 새로운 노드를 추가한 이후에도 완전 이진 트리를 유지해야 하는 경우에는 연결 리스트가 아닌 배열을 기반으로 트리를 구현해야 한다.
왼쪽/오른쪽 자식 노드의 index 값을 얻는 방법, 그리고 부모 노드의 index값을 얻는 방법
- 왼쪽 자식 노드의 인덱스 값 : 부모 노드의 인덱스 값 X 2
- 오른쪽 자식 노드의 인덱스 값 : 부모 노드의 인덱스 값 X 2 + 1
- 부모 노드의 인덱스 값 : 자식 노드의 인덱스 값 / 2
SimpleHeap.h
// SimpleHeap.h
#ifndef __SIMPLE_HEAP_H__
#define __SIMPLE_HEAP_H__
#define HEAP_LEN 100
typedef char* HData;
typedef int PriorityComp(HData d1, HData d2);
typedef struct _heap {
PriorityComp* comp;
int numOfData;
HData heapArr[HEAP_LEN];
} Heap;
void HeapInit(Heap* ph, PriorityComp pc);
int HIsEmpty(Heap* ph);
void HInsert(Heap* ph, HData data);
HData HDelete(Heap* ph);
#endifSimpleHeap.cpp
// SimpleHeap.cpp
#include "SimpleHeap.h"
// 힙의 초기화
void HeapInit(Heap* ph, PriorityComp pc) {
ph->numOfData = 0;
ph->comp = pc;
}
// 힙이 비었는지 확인
int HIsEmpty(Heap* ph) {
if (ph->numOfData == 0) {
return true;
}
return false;
}
// 부모 노드의 인덱스 값 반환
int GetParentIDX(int idx) {
return idx / 2;
}
// 왼쪽 자식 노드의 인덱스 값 반환
int GetLChildIDX(int idx) {
return idx * 2;
}
// 오른쪽 자식 노드의 인덱스 값 반환
int GetRChildIDX(int idx) {
return GetLChildIDX(idx) + 1;
}
// 두 개의 자식 노드 중 높은 우선순위의 자식 노드 인덱스 값 반환
int GetHiPriChildIDX(Heap* ph, int idx) {
// 자식 노드가 존재하지 않는다면
if (GetLChildIDX(idx) > ph->numOfData) {
return 0;
}
// 자식 노드가 왼쪽 자식 노드 하나만 존재한다면
else if (GetLChildIDX(idx) == ph->numOfData) {
return GetLChildIDX(idx);
}
// 자식 노드가 둘 다 존재한다면, 우선순위가 높은 index 반환
else {
if (ph->comp(ph->heapArr[GetLChildIDX(idx)],
ph->heapArr[GetRChildIDX(idx)]) < 0) {
return GetRChildIDX(idx);
}
return GetLChildIDX(idx);
}
}
// 힙에 데이터 저장
void HInsert(Heap* ph, HData data) {
// 새 노드가 저장될 인덱스 값을 idx에 저장
int idx = ph->numOfData + 1;
// 새 노드가 저장될 위치가 루트 노드의 위치가 아니라면 while문 반복
while (idx != 1) {
// 새 노드와 부모 노드의 우선순위 비교하여 새 노드의 우선순위가 높다면
if (ph->comp(data, ph->heapArr[GetParentIDX(idx)]) > 0) {
// 부모 노드를 한 레벨 내림, 실제로 내림
ph->heapArr[idx] = ph->heapArr[GetParentIDX(idx)];
// 새 노드를 한 레벨 올림, 실제로 올리지 않고 인덱스 값만 갱신
idx = GetParentIDX(idx);
}
// 새 노드의 우선순위가 높지 않다면
else {
break;
}
}
// 새 노드를 배열에 저장
ph->heapArr[idx] = data;
ph->numOfData++;
}
// 힙에서 데이터 삭제
HData HDelete(Heap* ph) {
// 반환을 위해 삭제할 데이터 저장
HData retData = ph->heapArr[1];
// 힙의 마지막 데이터 저장
HData lastElem = ph->heapArr[ph->numOfData];
// 마지막 데이터가 저장될 위치 정보가 담긴다.
int parentIdx = 1;
int childIdx;
// 루트 노드의 우선순위가 높은 자식 노드를 시작으로 반복 시작
while (childIdx = GetHiPriChildIDX(ph, parentIdx)) {
// 마지막 노드와 우선순위 비교
if (ph->comp(lastElem, ph->heapArr[childIdx]) >= 0) {
// 마지막 노드의 우선순위가 높으면 반복 탈출
break;
}
// 마지막 노드보다 우선순위가 높으니, 비교대상 데이터 위치를 한 레벨 올림
ph->heapArr[parentIdx] = ph->heapArr[childIdx];
// 마지막 노드가 저장될 위치정보를 한 레벨 내림
// 반복문을 탈출하면 parentIdx에는 마지막 데이터의 위치정보가 저장됨
parentIdx = childIdx;
}
// 마지막 데이터 최종 저장
ph->heapArr[parentIdx] = lastElem;
ph->numOfData--;
return retData;
}PriorityQueue.h
// PriorityQueue.h
#ifndef __PRIORITY_QUEUE_H__
#define __PRIORITY_QUEUE_H__
#include "SimpleHeap.h"
typedef Heap PQueue;
typedef HData PQData;
void PQueueInit(PQueue* ppq, PriorityComp pc);
int PQIsEmpty(PQueue* ppq);
void PEnqueue(PQueue* ppq, PQData data);
PQData PDequeue(PQueue* ppq);
#endifPriorityQueue.cpp
// PriorityQueue.cpp
#include "PriorityQueue.h"
#include "SimpleHeap.h"
void PQueueInit(PQueue* ppq, PriorityComp pc) {
HeapInit(ppq, pc);
}
int PQIsEmpty(PQueue* ppq) {
return HIsEmpty(ppq);
}
void PEnqueue(PQueue* ppq, PQData data) {
HInsert(ppq, data);
}
PQData PDequeue(PQueue* ppq) {
return HDelete(ppq);
}PriorityQueueMain.cpp
// PriorityQueueMain.cpp
#include <iostream>
#include <cstring>
#include "PriorityQueue.h"
#pragma warning(disable: 4996)
// 우선순위 비교 함수
int DataPriorityComp(char* str1, char* str2) {
return strlen(str2) - strlen(str1);
}
int main()
{
PQueue pq;
PQueueInit(&pq, DataPriorityComp);
PEnqueue(&pq, (char*)"c++ programming");
PEnqueue(&pq, (char*)"csharp coding");
PEnqueue(&pq, (char*)"Priority Queue");
PEnqueue(&pq, (char*)"Game Programming");
while (!PQIsEmpty(&pq)) {
printf("%s \n", PDequeue(&pq));
}
return 0;
}
/* 결과
csharp coding
Priority Queue
c++ programming
Game Programming
*/'Programming > Algorithm' 카테고리의 다른 글
| [Programming/Algorithm] 선택 정렬(Selection Sort) (0) | 2021.03.08 |
|---|---|
| [Programming/Algorithm] 버블 정렬(Bubble Sort) (0) | 2021.03.08 |
| [Programming/Algorithm] 퀵 정렬(Quick Sort) with Python (0) | 2021.02.10 |
| [Programming/Algorithm] 이진 탐색 알고리즘 (0) | 2021.02.09 |
| [Programming/Algorithm] 이진 탐색 트리(Binary Search Tree : BST) with Python (0) | 2021.02.09 |

