| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- jupyter lab
- Houdini
- c# 윈폼
- 포인터
- Flutter
- gitlab
- git
- c# 추상 클래스
- jupyter
- 다트 언어
- Python
- docker
- C++
- c언어
- dart 언어
- github
- Algorithm
- C언어 포인터
- 도커
- Data Structure
- HTML
- vim
- Unity
- c#
- 플러터
- 유니티
- 깃
- c# winform
- C# delegate
- 구조체
- Today
- Total
nomad-programmer
[Programming/Algorithm] 이진 탐색 트리(Binary Search Tree : BST) with Python 본문
[Programming/Algorithm] 이진 탐색 트리(Binary Search Tree : BST) with Python
scii 2021. 2. 9. 20:07이진 탐색 트리의 특징
이진 탐색 트리는 두 가지 중요한 특징이 있다.
첫째, 어떤 특정 노드를 선택했을 때 그 노드를 기준으로 왼쪽 서브 트리에 존재하는 노드의 모든 데이터는 기준 노드의 값보다 작고, 오른쪽 서브 트리에 있는 노드의 모든 데이터는 기준 노드의 값보다 크다는 것이다.
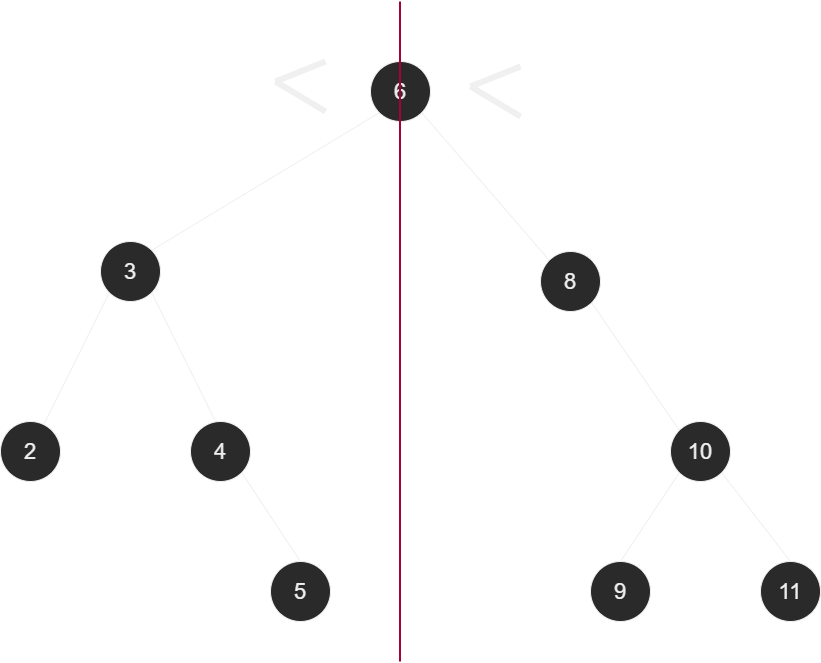
루트 노드를 기준으로 왼쪽 서브 트리의 모든 데이터는 루트 노드의 데이터인 6보다 작다. 오른쪽 서브 트리의 모든 데이터는 6보다 크다.

위의 그림에서 루트 노드의 왼쪽 자식 노드가 기준 노드일 때, 기준 노드의 왼쪽 서브 트리의 모든 데이터는 기준 노드의 데이터인 3보다 작다. 오른쪽 서브 트리의 모든 데이터는 3보다 크다. 기준 노드가 루트 노드의 오른쪽 자식 노드일 때도 같은 조건이 성립한다.
즉, 특정 노드를 기준으로 그 노드의 서브 트리도 모두 이진 탐색 트리인 것을 알 수 있다.
이진 탐색 트리의두 번째 특징은 이진 탐색 트리는 중복 데이터를 가질 수 없다는 것이다. 첫 번째 특징을 생각해 보면 당연하다. 특정 노드가 기준일 때 왼쪽 서브 트리의 모든 데이터는 노드 데이터보다 작고 오른쪽 서브 트리의 모든 데이터는 노드 데이터보다 커야하므로 값이 같은 데이터는 존재할 수 없다.
이진 탐색 트리의 구현
이진 탐색 트리의 추상 자료형을 살펴보자.
- BST. insert(data) -> None
- 이진 탐색 트리에 데이터 삽입
- BST. search(target) -> node
- 이진 탐색 트리에서 대상 데이터를 가진 노드를 반환. 데이터가 없으면 None을 반환.
- BST. remove(target) -> node
- 이진 탐색 트리에 대상 데이터가 있다면 데이터를 가진 노드를 삭제하면서 반환.
- 데이터가 없으면 None을 반환.
- BST. insert_node(node) -> None
- 데이터가 아니라 노드를 삽입. remove에서 반환받은 노드의 데이터를 수정한 후 다시 삽입할 때 사용.
BST에서 insert()와 search(0 메서드는 구현하기가 어렵지 않지만, remove() 메서드는 구현하기가 매우 까다롭다. 그 이유는 삭제하려는 노드가 leaf 노드인지, 자식 노드가 하나인지 두 개인지에 따라 삭제하는 방법이 다르기 때문이다.
이진 트리 관련 메서드
class BST:
def __init__(self):
self.root = None
def get_root(self):
return self.root
def preorder_traverse(self, cur, f):
if not cur:
return
f(cur.data)
self.preorder_traverse(cur.left, f)
self.preorder_traverse(cur.right, f)insert() 메서드
삽입하려는 데이터를 루트 노드부터 시작해 차례대로 비교해 내려간다. 삽입 데이터가 노드의 데이터보다 작으면 왼쪽 자식 노드로 이동하고, 노드의 데이터보다 크면 오른쪽 자식 노드로 이동해 다시 비교한다.
class TreeNode:
def __init__(self):
self.data = 0
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def get_root(self):
return self.root
def preorder_traverse(self, cur, f):
if not cur:
return
f(cur.data)
self.preorder_traverse(cur.left, f)
self.preorder_traverse(cur.right, f)
def insert(self, data):
new_node = TreeNode()
new_node.data = data
cur = self.root
# 루트 노드가 없을 때
if cur == None:
self.root = new_node
return
# 삽입할 노드의 위치를 찾아 삽입
while True:
# parent는 현재 순회중인 노드의 부모 노드를 가리킴
parent = cur
# 삽입할 데이터가 현재 노드 데이터보다 작을 때
if data < cur.data:
cur = cur.left
# 왼쪽 서브 트리가 None이면 새 노드를 위치시킨다.
if not cur:
parent.left = new_node
return
# 삽입할 데이터가 현재 노드 데이터보다 클 때
else:
cur = cur.right
# 오른쪽 서브 트리가 None이면 새 노드를 위치시킨다.
if not cur:
parent.right = new_node
returnsearch() 메서드
search() 메서드는 insert() 메서드와 유사하다. 대상 데이터를 루트 노드부터 비교하면서 내려온다. 노드의 데이터가 대상 데이터와 같다면 노드를 반환한다. 빈 노드를 만날 때까지 대상 데이터와 같은 노드를 만나지 못하면 None을 반환한다.
def search(self, target):
cur = self.root
while cur:
# 대상 데이터를 찾으면 노드 반환
if target == cur.data:
return cur
# 대상 데이터가 노드 데이터보다 작으면
# 왼쪽 자식 노드로 이동
elif target < cur.data:
cur = cur.left
# 대상 데이터가 노드 데이터보다 크면
# 오른쪽 자식 노드로 이동
elif target > cur.data:
cur = cur.right
# while 문을 빠져나온 경우
# 대상 데이터가 트리 안에 없다.
return curremove() 메서드
remove() 메서드는 재귀 함수를 사용해 구현해야 한다. 먼저 지우려는 대상 데이터를 찾는다. 다음으로 삭제 노드의 상태에 따라 세 가지 경우로 나누어 지운다.
- 삭제 노드가 리프 노드일 때
- 삭제 노드의 자식 노드가 하나일 때
- 삭제 노드의 자식 노드가 두 개일 때
def remove(self, target):
# 루트 노드의 변경 가능성이 있으므로 루트를 업데이트해야 한다.
self.root, removed_node = self.__remove_recursion(self.root, target)
# 삭제된 노드의 자식 노드를 None으로 만든다.
removed_node.left = removed_node.right = None
return removed_noderemove() 메서드 안에서 재귀 함수인 __remove_recursion() 메서드를 호출한다. 이때 __remove_recursion() 함수 앞에 언더바(_)가 두 개 붙은 이유는 이 함수가 클래스 내부에서만 쓰이는 함수이기 때문이다. 유저 프로그래머가 실수로 호출하지 않도록 정보 은닉을 한 것이다. __remove_recursion() 메서드는 메서드를 호출한 노드를 루트 노드로하여 대상 노드를 삭제한 후 트리의 업데이트된 루트 노드와 삭제된 노드를 반환한다.
삭제 노드가 루트 노드인 경우 루트 노드가 변경될 수 있으므로 반드시 루트 노드를 업데이트 해야 한다. remove() 메서드는 __remove_recursion() 메서드에서 반환받은 삭제 노드 removed_node만 반환하면 된다.
def __remove_recursion(self, cur, target):
# 대상 데이터가 트리 안에 없을 때
if cur is None:
return None, None
# 대상 데이터가 노드 데이터보다 작으면
# 노드의 왼쪽 자식에서 대상 데이터를 가진 노드를 지운다
elif target < cur.data:
cur.left, rem_node = self.__remove_recursion(cur.left, target)
# 대상 데이터가 노드 데이터보다 크면
# 노드의 오른쪽 자식에서 대상 데이터를 가진 노드를 지운다.
elif target > cur.data:
cur.right, rem_node = self.__remove_recursion(cur.right, target)
else:
# leaf 노드 일 때
if not cur.left and not cur.right:
rem_node = cur
cur = None
# 자식 노드가 하나일 때 : 왼쪽 자식
elif not cur.right:
rem_node = cur
cur = cur.left
# 자식 노드가 하나일 때 : 오른쪽 자식
elif not cur.left:
rem_node = cur
cur = cur.right
# 자식 노드가 두 개일 때
else:
# 대체 노드를 찾는다.
replace = cur.left
while replace.right:
replace = replace.right
# 삭제 노드와 대체 노드의 값을 교환
cur.data, replace.data = replace.data, cur.data
# 대체 노드를 삭제하려면 삭제된 노드를 받아온다
cur.left, rem_node = self.__remove_recursion(cur.left, replace.data)
# 삭제 노드가 루트 노드일 경우, 루트가 변경될 수 있기 때문에
# 삭제 후 현재 루트를 반환
return cur, rem_node탈출 조건은 대상 데이터가 트리 안에 없거나 대상 데이터를 찾을 때이다.
insert_node() 메서드
remove() 메서드에서 반환받은 삭제 노드를 수정한 다음 이진 탐색 트리에 다시 삽입하는 insert_node() 메서드를 만들어보자.
def insert_node(self, node):
cur = self.root
if cur is None:
self.root = node
return
while True:
parent = cur
if node.data < cur.data:
cur = cur.left
if not cur:
parent.left = node
return
else:
cur = cur.right
if not cur:
parent.right = node
returninsert_node() 메서드는 인자로 데이터 대신 노드를 받는다. remove() 메서드에서 반환 받은 노드를 수정한 다음 이를 다시 삽입하기 위한 메서드이다. 이 메서드를 이용하면 객체 생성에 따른 부담을 줄일 수 있다.
class TreeNode:
def __init__(self):
self.data = 0
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
def get_root(self):
return self.root
def preorder_traverse(self, cur, f):
if not cur:
return
f(cur.data)
self.preorder_traverse(cur.left, f)
self.preorder_traverse(cur.right, f)
def insert(self, data):
new_node = TreeNode()
new_node.data = data
cur = self.root
# 루트 노드가 없을 때
if cur == None:
self.root = new_node
return
# 삽입할 노드의 위치를 찾아 삽입
while True:
# parent는 현재 순회중인 노드의 부모 노드를 가리킴
parent = cur
# 삽입할 데이터가 현재 노드 데이터보다 작을 때
if data < cur.data:
cur = cur.left
# 왼쪽 서브 트리가 None이면 새 노드를 위치시킨다.
if not cur:
parent.left = new_node
return
# 삽입할 데이터가 현재 노드 데이터보다 클 때
else:
cur = cur.right
# 오른쪽 서브 트리가 None이면 새 노드를 위치시킨다.
if not cur:
parent.right = new_node
return
def search(self, target):
cur = self.root
while cur:
# 대상 데이터를 찾으면 노드 반환
if target == cur.data:
return cur
# 대상 데이터가 노드 데이터보다 작으면
# 왼쪽 자식 노드로 이동
elif target < cur.data:
cur = cur.left
# 대상 데이터가 노드 데이터보다 크면
# 오른쪽 자식 노드로 이동
elif target > cur.data:
cur = cur.right
# while 문을 빠져나온 경우
# 대상 데이터가 트리 안에 없다.
return cur
def remove(self, target):
# 루트 노드의 변경 가능성이 있으므로 루트를 업데이트해야 한다.
self.root, removed_node = self.__remove_recursion(self.root, target)
# 삭제된 노드의 자식 노드를 None으로 만든다.
removed_node.left = removed_node.right = None
return removed_node
def __remove_recursion(self, cur, target):
# 대상 데이터가 트리 안에 없을 때
if cur is None:
return None, None
# 대상 데이터가 노드 데이터보다 작으면
# 노드의 왼쪽 자식에서 대상 데이터를 가진 노드를 지운다
elif target < cur.data:
cur.left, rem_node = self.__remove_recursion(cur.left, target)
# 대상 데이터가 노드 데이터보다 크면
# 노드의 오른쪽 자식에서 대상 데이터를 가진 노드를 지운다.
elif target > cur.data:
cur.right, rem_node = self.__remove_recursion(cur.right, target)
else:
# leaf 노드 일 때
if not cur.left and not cur.right:
rem_node = cur
cur = None
# 자식 노드가 하나일 때 : 왼쪽 자식
elif not cur.right:
rem_node = cur
cur = cur.left
# 자식 노드가 하나일 때 : 오른쪽 자식
elif not cur.left:
rem_node = cur
cur = cur.right
# 자식 노드가 두 개일 때
else:
# 대체 노드를 찾는다.
replace = cur.left
while replace.right:
replace = replace.right
# 삭제 노드와 대체 노드의 값을 교환
cur.data, replace.data = replace.data, cur.data
# 대체 노드를 삭제하려면 삭제된 노드를 받아온다
cur.left, rem_node = self.__remove_recursion(cur.left, replace.data)
# 삭제 노드가 루트 노드일 경우, 루트가 변경될 수 있기 때문에
# 삭제 후 현재 루트를 반환
return cur, rem_node
def insert_node(self, node):
cur = self.root
if cur is None:
self.root = node
return
while True:
parent = cur
if node.data < cur.data:
cur = cur.left
if not cur:
parent.left = node
return
else:
cur = cur.right
if not cur:
parent.right = node
return
if __name__ == '__main__':
bst = BST()
bst.insert(6)
bst.insert(3)
bst.insert(2)
bst.insert(4)
bst.insert(5)
bst.insert(8)
bst.insert(10)
bst.insert(9)
bst.insert(11)
f = lambda x: print(x, end=' ')
bst.preorder_traverse(bst.get_root(), f)
print()
bst.remove(9)
bst.preorder_traverse(bst.get_root(), f)
print()
# 이진 탐색 트리에서 6 노드를 삭제
node = bst.remove(6)
# 반환받은 삭제 노드의 데이터를 7로 변경
node.data = 7
# 변경된 노드를 이진 탐색 트리에 다시 삽입
bst.insert_node(node)
bst.preorder_traverse(bst.get_root(), f)
print()
""" 결과
6 3 2 4 5 8 10 9 11
6 3 2 4 5 8 10 11
5 3 2 4 8 7 10 11
"""'Programming > Algorithm' 카테고리의 다른 글
| [Programming/Algorithm] 우선순위 큐와 Heap 자료구조 (0) | 2021.03.07 |
|---|---|
| [Programming/Algorithm] 퀵 정렬(Quick Sort) with Python (0) | 2021.02.10 |
| [Programming/Algorithm] 이진 탐색 알고리즘 (0) | 2021.02.09 |
| [Programming/Algorithm] 이진 트리 with Python (0) | 2021.02.09 |
| [Programming/Algorithm] 간단한 양방향 List 자료구조의 구현 (0) | 2021.01.24 |


