| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 플러터
- C언어 포인터
- c# 추상 클래스
- 포인터
- C++
- docker
- 다트 언어
- c# 윈폼
- gitlab
- vim
- Flutter
- Algorithm
- 깃
- 구조체
- Data Structure
- C# delegate
- jupyter lab
- Python
- Unity
- HTML
- c# winform
- github
- 도커
- c#
- git
- jupyter
- c언어
- 유니티
- dart 언어
- Houdini
Archives
- Today
- Total
nomad-programmer
[Programming/Algorithm] 이진 트리 with Python 본문
Python으로 만드는 이진 트리 알고리즘
class TreeNode:
def __init__(self):
self.__data = None
self.__left = None
self.__right = None
def __del__(self):
print('TreeNode of {} is deleted'.format(self.data))
@property
def data(self):
return self.__data
@data.setter
def data(self, data):
self.__data = data
@property
def left(self):
return self.__left
@left.setter
def left(self, left):
self.__left = left
@property
def right(self):
return self.__right
@right.setter
def right(self, right):
self.__right = right
class BinaryTree:
def __init__(self):
self.root = None
# root 노드 반환
def get_root(self):
return self.root
# root 노드 설정
def set_root(self, r):
self.root = r
# 새로운 노드를 만들어 반환
def make_node(self):
new_node = TreeNode()
return new_node
# 노드의 데이터 반환
def get_node_data(self, cur):
return cur.data()
# 노드의 데이터 설정
def set_node_data(self, cur, data):
cur.data = data
# 왼쪽 서브 트리 반환
def get_left_sub_tree(self, cur):
return cur.left
# 오른쪽 서브 트리 반환
def get_right_sub_tree(self, cur):
return cur.right
# 왼쪽 서브 트리 만듦
def make_left_sub_tree(self, cur, left):
cur.left = left
# 오른족 서브 트리 만듦
def make_right_sub_tree(self, cur, right):
cur.right = right
if __name__ == '__main__':
# 이진 트리 객체 생성
bt = BinaryTree()
# 노드 생성
n1 = bt.make_node()
bt.set_node_data(n1, 1)
n2 = bt.make_node()
bt.set_node_data(n2, 2)
n3 = bt.make_node()
bt.set_node_data(n3, 3)
n4 = bt.make_node()
bt.set_node_data(n4, 4)
n5 = bt.make_node()
bt.set_node_data(n5, 5)
n6 = bt.make_node()
bt.set_node_data(n6, 6)
n7 = bt.make_node()
bt.set_node_data(n7, 7)
# 노드 1을 root 노드로 설정
bt.set_root(n1)
# root 노드의 왼쪽 자식 노드로 노드2 설정
bt.make_left_sub_tree(n1, n2)
# root 노드의 오른족 자식 노드로 노드3 설정
bt.make_right_sub_tree(n1, n3)
bt.make_left_sub_tree(n2, n4)
bt.make_right_sub_tree(n2, n5)
bt.make_left_sub_tree(n3, n6)
bt.make_right_sub_tree(n3, n7)위의 코드를 실행하면 다음과 같은 이진 트리가 구성된다.
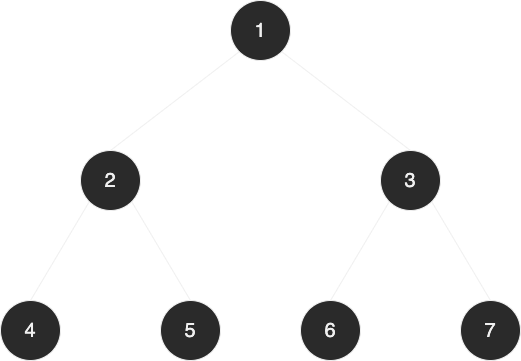
트리의 순회
트리의 모든 노드를 중복하지 않으면서 방문하는 것을 순회(traversal)이라고 한다. 데이터를 저장만 하고 찾을 수 없다면 아무 소용이 없다. 그만큼 순회는 굉장히 중요한 개념이다.
순회하는 방법에는 세 가지가 있다.
- 전위 순회(preorder traversal)
- root -> 왼쪽 서브 트리 -> 오른쪽 서브 트리
- 중위 순회(inorder traversal)
- 왼쪽 서브 트리 -> root -> 오른쪽 서브 트리
- 후위 순회(postorder traversal)
- 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> root
전위 순회든 중위 순회든 후위 순회든 왼쪽 서브 트리와 오른쪽 서브 트리가 들어 있다. 목적은 모든 노드를 방문하는 것으므로 서브 트리의 모든 노드도 방문해야 한다.
방문하는 방법은 재귀를 통해 모든 노드를 방문할 수 있다. 서브 트리도 이진 트리이므로 서브 트리에서도 순회마다 순서를 맞춰 재귀적으로 노드를 방문하는 것이다.
이진 트리를 어떻게 순회하는지 다음 그림으로 살펴보자.
전위 순회(preorder traverse)

중위 순회(inorder traverse)

후위 순회(postorder traverse)

재귀 함수를 이용해 각 순회를 구현해 보자.
class TreeNode:
def __init__(self):
self.__data = None
self.__left = None
self.__right = None
def __del__(self):
pass
@property
def data(self):
return self.__data
@data.setter
def data(self, data):
self.__data = data
@property
def left(self):
return self.__left
@left.setter
def left(self, left):
self.__left = left
@property
def right(self):
return self.__right
@right.setter
def right(self, right):
self.__right = right
class BinaryTree:
def __init__(self):
self.root = None
# root 노드 반환
def get_root(self):
return self.root
# root 노드 설정
def set_root(self, r):
self.root = r
# 새로운 노드를 만들어 반환
def make_node(self):
new_node = TreeNode()
return new_node
# 노드의 데이터 반환
def get_node_data(self, cur):
return cur.data()
# 노드의 데이터 설정
def set_node_data(self, cur, data):
cur.data = data
# 왼쪽 서브 트리 반환
def get_left_sub_tree(self, cur):
return cur.left
# 오른쪽 서브 트리 반환
def get_right_sub_tree(self, cur):
return cur.right
# 왼쪽 서브 트리 만듦
def make_left_sub_tree(self, cur, left):
cur.left = left
# 오른족 서브 트리 만듦
def make_right_sub_tree(self, cur, right):
cur.right = right
# 전위 순회로 트리를 순회
def preorder_traverse(self, cur, func):
# 만약 방문한 노드가 빈 노드일 때
if not cur:
return
# 먼저 방문 노드의 데이터를 인자로 함수 호출
func(cur.data)
# 왼쪽 서브 트리 순회
self.preorder_traverse(cur.left, func)
# 오른쪽 서브 트리 순회
self.preorder_traverse(cur.right, func)
# 중위 순회로 트리를 순회
def inorder_traverse(self, cur, func):
if not cur:
return
# 먼저 왼쪽 서브 트리 순회
self.inorder_traverse(cur.left, func)
# 왼쪽 서브 트리 모두 순회 후, 방문 노드의 데이터를 인자로 함수 호출
func(cur.data)
# 오른쪽 서브 트리 순회
self.inorder_traverse(cur.right, func)
# 후위 순회로 트리를 순회
def postorder_traverse(self, cur, func):
if not cur:
return
# 왼쪽 서브 트리 순회
self.postorder_traverse(cur.left, func)
# 오른쪽 서브 트리 순회
self.postorder_traverse(cur.right, func)
# 왼쪽 서브 트리와 오른쪽 서브 트리 모두 순회한 후
# 마지막으로 방문 노드의 데이터를 인자로 함수 호출
func(cur.data)
if __name__ == '__main__':
# 이진 트리 객체 생성
bt = BinaryTree()
# 노드 생성
n1 = bt.make_node()
bt.set_node_data(n1, 1)
n2 = bt.make_node()
bt.set_node_data(n2, 2)
n3 = bt.make_node()
bt.set_node_data(n3, 3)
n4 = bt.make_node()
bt.set_node_data(n4, 4)
n5 = bt.make_node()
bt.set_node_data(n5, 5)
n6 = bt.make_node()
bt.set_node_data(n6, 6)
n7 = bt.make_node()
bt.set_node_data(n7, 7)
# 노드 1을 root 노드로 설정
bt.set_root(n1)
# root 노드의 왼쪽 자식 노드로 노드2 설정
bt.make_left_sub_tree(n1, n2)
# root 노드의 오른족 자식 노드로 노드3 설정
bt.make_right_sub_tree(n1, n3)
bt.make_left_sub_tree(n2, n4)
bt.make_right_sub_tree(n2, n5)
bt.make_left_sub_tree(n3, n6)
bt.make_right_sub_tree(n3, n7)
# 방문 노드의 데이터를 출력하는 람다 함수
f = lambda a: print(a, end=' ')
# 전위 순회
# 기대 출력 값: 1 2 4 5 3 6 7
bt.preorder_traverse(bt.get_root(), f)
print()
# 중위 순회
# 기대 출력 값: 4 2 5 1 6 3 7
bt.inorder_traverse(bt.get_root(), f)
print()
# 후위 순회
# 기대 출력 값: 4 5 2 6 7 3 1
bt.postorder_traverse(bt.get_root(), f)
print()
""" 결과
1 2 4 5 3 6 7
4 2 5 1 6 3 7
4 5 2 6 7 3 1
"""전위 순회, 중위 순회, 후위 순회 모두 재귀 함수를 통해 순회 순서를 구현한다. 탈출 조건은 빈 노드일 때이다. 인자 func는 데이터 처리 함수로 방문 노드의 데이터를 인자로 받아 실행된다.
재귀 함수는 분할 정복 알고리즘 등 여러 알고리즘을 구현하는 데 요긴하게 쓰인다.
트리는 삽입은 물론 탐색과 삭제도 빨라 프로그래밍에서 자주 사용되는 자료 구조이다.
'Programming > Algorithm' 카테고리의 다른 글
| [Programming/Algorithm] 우선순위 큐와 Heap 자료구조 (0) | 2021.03.07 |
|---|---|
| [Programming/Algorithm] 퀵 정렬(Quick Sort) with Python (0) | 2021.02.10 |
| [Programming/Algorithm] 이진 탐색 알고리즘 (0) | 2021.02.09 |
| [Programming/Algorithm] 이진 탐색 트리(Binary Search Tree : BST) with Python (0) | 2021.02.09 |
| [Programming/Algorithm] 간단한 양방향 List 자료구조의 구현 (0) | 2021.01.24 |
Comments


